Stack and Queue in Data Structure with Coding

Main Topic: Stack and Queue in Data Structure with Coding

Article Outline

Introduction to Stack and Queue Data Structures
What is a Stack Data Structure?
Key Characteristics of Stacks
Stack Operations Explained
1. 4.1 Push Operation
2. 4.2 Pop Operation
3. 4.3 Peek/Top Operation
Real-World Applications of Stacks
Stack Implementation in Code
1. 6.1 Array-Based Stack Implementation
2. 6.2 Linked List-Based Stack Implementation
What is a Queue Data Structure?
Key Characteristics of Queues
Queue Operations Explained
1. 9.1 Enqueue Operation
2. 9.2 Dequeue Operation
3. 9.3 Front and Rear Operations
Types of Queues
1. 10.1 Simple Queue
2. 10.2 Circular Queue
3. 10.3 Priority Queue
Real-World Applications of Queues
Queue Implementation in Code
1. 12.1 Array-Based Queue Implementation
2. 12.2 Linked List-Based Queue Implementation
Stack vs Queue: Key Differences
Performance Analysis and Time Complexity
Best Practices and Common Pitfalls
Conclusion
FAQs

Stack and Queue in Data Structure with Coding: A Complete Guide

Introduction to Stack and Queue Data Structures

Have you ever wondered how your computer manages multiple tasks simultaneously or how the "undo" function in your favorite text editor works? The answer lies in two fundamental data structures: stacks and queues. These linear data structures are the backbone of countless algorithms and applications in computer science.

Think of data structures as organized containers that help us store and manipulate information efficiently. Among these, stacks and queues stand out as essential tools that every programmer must master. They're like the Swiss Army knives of programming – simple in concept yet incredibly powerful in application.

In this comprehensive guide, we'll dive deep into both structures, explore their characteristics, understand their operations, and most importantly, see how to implement them through practical coding examples. Whether you're a beginner trying to grasp these concepts or an experienced developer looking to refresh your knowledge, this article has something for everyone.

What is a Stack Data Structure?

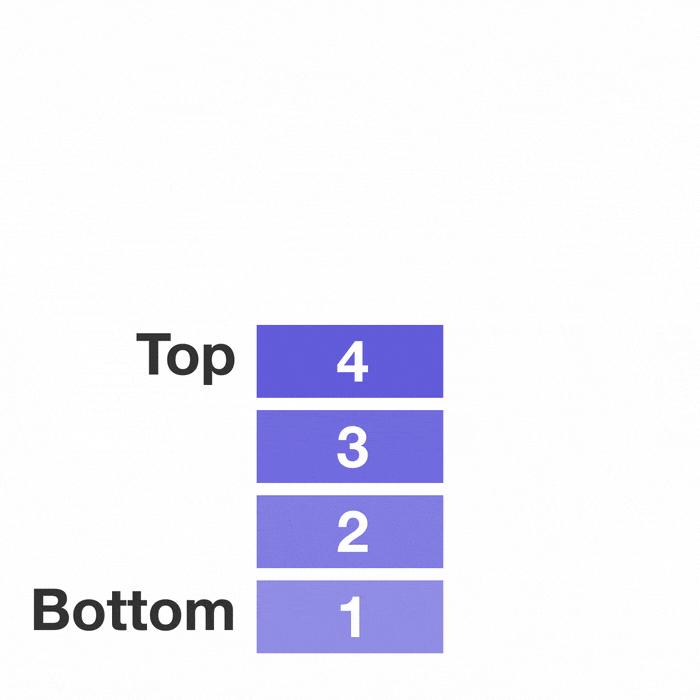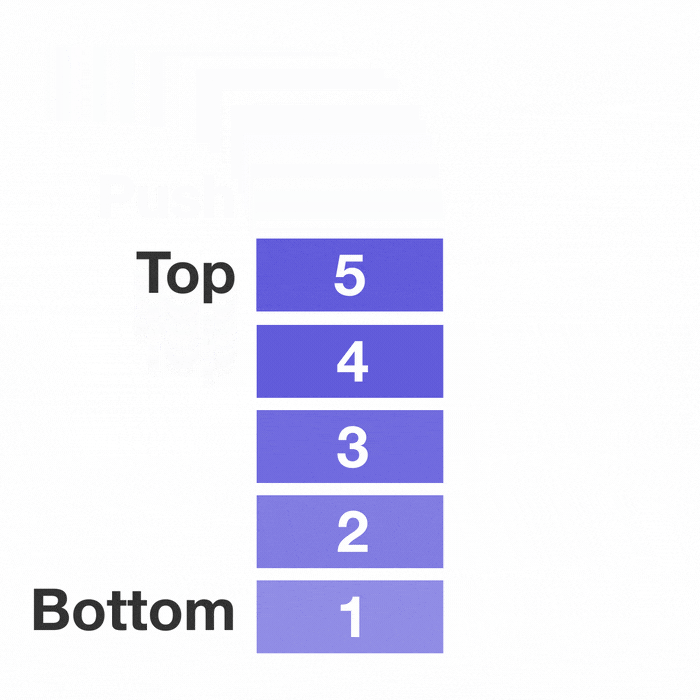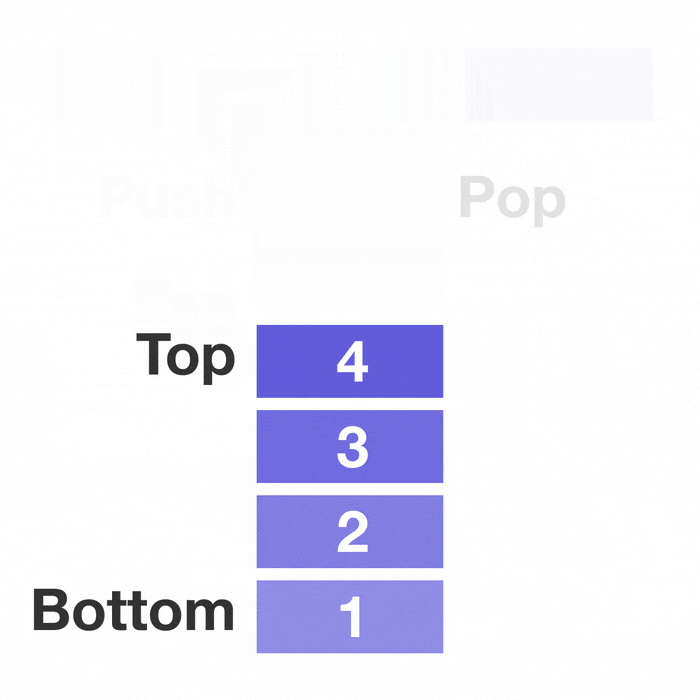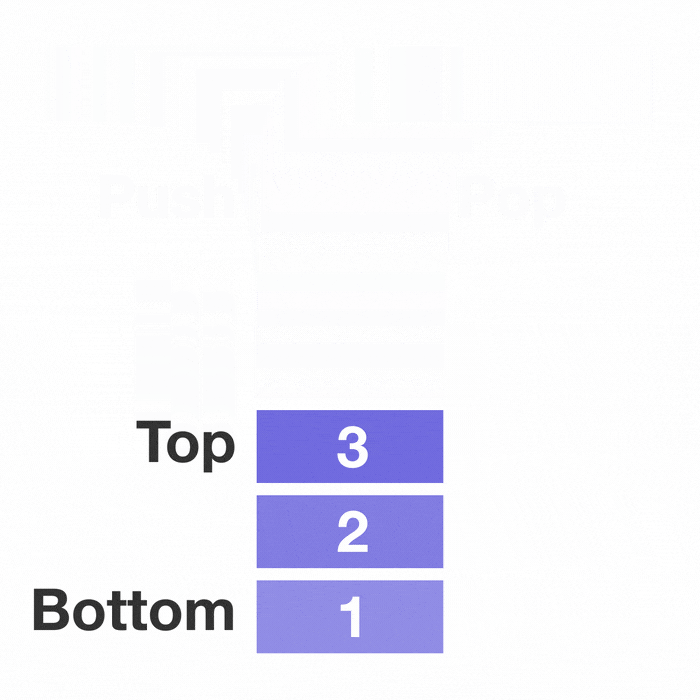
A stack is a linear data structure that follows the Last-In-First-Out (LIFO) principle. Imagine a stack of plates in your kitchen – you add new plates to the top, and when you need one, you take it from the top as well. That's exactly how a stack data structure operates!

The beauty of a stack lies in its simplicity. You can only access the element at the top, making it a restricted data structure. This restriction might seem limiting, but it's actually what makes stacks so powerful for specific applications.

Key Characteristics of Stacks

LIFO Ordering: The last element inserted is the first one to be removed
Single Access Point: You can only access the top element
Dynamic Size: Most stack implementations can grow and shrink during runtime
Memory Efficient: Only stores the necessary elements without wasting space

These characteristics make stacks perfect for scenarios where you need to reverse operations or track a sequence of actions.

Stack Operations Explained

Push Operation

The push operation adds an element to the top of the stack. It's like placing a new book on top of a pile – the new book becomes the topmost item. When we push an element, we increment the stack pointer to the new top position.

Pop Operation

Pop removes and returns the top element from the stack. Continuing our book analogy, it's like taking the top book from the pile. After popping, the stack pointer moves down to point to the new top element.

Peek/Top Operation

The peek (or top) operation allows you to view the top element without removing it. Think of it as looking at the title of the top book without actually taking it from the pile. This operation is read-only and doesn't modify the stack.

Real-World Applications of Stacks

Function Call Management: Every time you call a function, the system uses a call stack to keep track of function calls
Undo Operations: Text editors, image editors, and many applications use stacks to implement undo functionality
Expression Evaluation: Calculators use stacks to evaluate mathematical expressions
Browser History: The back button functionality often uses stack-like behavior
Syntax Parsing: Compilers use stacks to check balanced parentheses and parse code

Stack Implementation in Code

Array-Based Stack Implementation

Let's implement a stack using arrays in Python:

class ArrayStack:
    def __init__(self, capacity=10):
        self.capacity = capacity
        self.stack = [None] * capacity
        self.top = -1
    
    def is_empty(self):
        return self.top == -1
    
    def is_full(self):
        return self.top == self.capacity - 1
    
    def push(self, item):
        if self.is_full():
            raise Exception("Stack Overflow")
        self.top += 1
        self.stack[self.top] = item
    
    def pop(self):
        if self.is_empty():
            raise Exception("Stack Underflow")
        item = self.stack[self.top]
        self.top -= 1
        return item
    
    def peek(self):
        if self.is_empty():
            raise Exception("Stack is empty")
        return self.stack[self.top]
    
    def size(self):
        return self.top + 1

# Example usage
stack = ArrayStack()
stack.push(10)
stack.push(20)
stack.push(30)
print(stack.pop())  # Output: 30
print(stack.peek()) # Output: 20

Linked List-Based Stack Implementation

Here's a more flexible implementation using linked lists:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedListStack:
    def __init__(self):
        self.top = None
        self.size_count = 0
    
    def is_empty(self):
        return self.top is None
    
    def push(self, item):
        new_node = Node(item)
        new_node.next = self.top
        self.top = new_node
        self.size_count += 1
    
    def pop(self):
        if self.is_empty():
            raise Exception("Stack Underflow")
        item = self.top.data
        self.top = self.top.next
        self.size_count -= 1
        return item
    
    def peek(self):
        if self.is_empty():
            raise Exception("Stack is empty")
        return self.top.data
    
    def size(self):
        return self.size_count

# Example usage
linked_stack = LinkedListStack()
linked_stack.push("First")
linked_stack.push("Second")
print(linked_stack.pop())  # Output: Second

What is a Queue Data Structure?

A queue is a linear data structure that follows the First-In-First-Out (FIFO) principle. Picture a line of people waiting at a coffee shop – the first person to join the line is the first one to be served. This is exactly how queues work in programming!

Unlike stacks, queues have two distinct ends: the front (where elements are removed) and the rear (where elements are added). This dual-access approach makes queues perfect for managing processes that need to be handled in order.

Key Characteristics of Queues

FIFO Ordering: First element in is the first element out
Two Access Points: Front for removal, rear for insertion
Sequential Processing: Elements are processed in the order they arrive
Fairness: No element can "cut in line" – everyone waits their turn

Queue Operations Explained

Enqueue Operation

Enqueue adds an element to the rear of the queue. It's like a new customer joining the back of the line at a store. The element becomes the last in line to be processed.

Dequeue Operation

Dequeue removes and returns the element from the front of the queue. This is equivalent to serving the customer who has been waiting the longest. After dequeuing, the next element in line becomes the new front.

Front and Rear Operations

Front: Returns the element at the front without removing it
Rear: Returns the element at the rear without removing it

Types of Queues

Simple Queue

The basic queue we've discussed, with straightforward FIFO behavior. Elements are added at the rear and removed from the front.

Circular Queue

A circular queue connects the rear back to the front, creating a circular structure. This eliminates the problem of unused space in array-based implementations.

Priority Queue

In a priority queue, elements have associated priorities. Higher priority elements are served before lower priority ones, regardless of their arrival time.

Real-World Applications of Queues

Operating System Scheduling: Process scheduling uses queues to manage task execution
Print Job Management: Printers use queues to handle multiple print requests
Network Packet Handling: Routers use queues to manage data packet transmission
Customer Service Systems: Call centers use queues to manage incoming calls
Breadth-First Search: Graph algorithms use queues for level-by-level traversal

Queue Implementation in Code

Array-Based Queue Implementation

Here's a simple array-based queue implementation:

class ArrayQueue:
    def __init__(self, capacity=10):
        self.capacity = capacity
        self.queue = [None] * capacity
        self.front = 0
        self.rear = -1
        self.size_count = 0
    
    def is_empty(self):
        return self.size_count == 0
    
    def is_full(self):
        return self.size_count == self.capacity
    
    def enqueue(self, item):
        if self.is_full():
            raise Exception("Queue Overflow")
        self.rear = (self.rear + 1) % self.capacity
        self.queue[self.rear] = item
        self.size_count += 1
    
    def dequeue(self):
        if self.is_empty():
            raise Exception("Queue Underflow")
        item = self.queue[self.front]
        self.queue[self.front] = None
        self.front = (self.front + 1) % self.capacity
        self.size_count -= 1
        return item
    
    def peek_front(self):
        if self.is_empty():
            raise Exception("Queue is empty")
        return self.queue[self.front]
    
    def size(self):
        return self.size_count

# Example usage
queue = ArrayQueue()
queue.enqueue("A")
queue.enqueue("B")
queue.enqueue("C")
print(queue.dequeue())  # Output: A
print(queue.peek_front())  # Output: B

Linked List-Based Queue Implementation

A more flexible implementation using linked lists:

class QueueNode:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedListQueue:
    def __init__(self):
        self.front = None
        self.rear = None
        self.size_count = 0
    
    def is_empty(self):
        return self.front is None
    
    def enqueue(self, item):
        new_node = QueueNode(item)
        if self.is_empty():
            self.front = self.rear = new_node
        else:
            self.rear.next = new_node
            self.rear = new_node
        self.size_count += 1
    
    def dequeue(self):
        if self.is_empty():
            raise Exception("Queue Underflow")
        item = self.front.data
        self.front = self.front.next
        if self.front is None:
            self.rear = None
        self.size_count -= 1
        return item
    
    def peek_front(self):
        if self.is_empty():
            raise Exception("Queue is empty")
        return self.front.data
    
    def peek_rear(self):
        if self.is_empty():
            raise Exception("Queue is empty")
        return self.rear.data
    
    def size(self):
        return self.size_count

# Example usage
linked_queue = LinkedListQueue()
linked_queue.enqueue(100)
linked_queue.enqueue(200)
print(linked_queue.dequeue())  # Output: 100
print(linked_queue.peek_front())  # Output: 200

Stack vs Queue: Key Differences

Aspect	Stack	Queue
Order	LIFO (Last-In-First-Out)	FIFO (First-In-First-Out)
Access Points	One (top only)	Two (front and rear)
Main Operations	Push, Pop, Peek	Enqueue, Dequeue, Front
Use Cases	Undo operations, function calls	Process scheduling, buffering
Memory Pattern	Grows upward	Linear progression

Performance Analysis and Time Complexity

Both stacks and queues offer excellent performance characteristics:

Stack Operations

Push: O(1)
Pop: O(1)
Peek: O(1)
Space Complexity: O(n)

Queue Operations

Enqueue: O(1)
Dequeue: O(1)
Front/Rear: O(1)
Space Complexity: O(n)

The constant time complexity makes both data structures highly efficient for their intended operations.

Best Practices and Common Pitfalls

Best Practices

Always check for empty conditions before popping or dequeuing
Use appropriate size limits to prevent memory overflow
Choose the right implementation (array vs. linked list) based on your needs
Implement proper error handling for edge cases

Common Pitfalls

Forgetting to check for stack overflow or underflow
Not handling empty queue/stack conditions
Mixing up LIFO and FIFO concepts
Not considering thread safety in concurrent environments

Conclusion

Stacks and queues are fundamental building blocks in computer science that power countless applications we use daily. While they might seem simple on the surface, their elegance lies in their focused approach to solving specific types of problems.

Stacks, with their LIFO nature, excel at managing temporary data and reversible operations. Queues, following FIFO principles, are perfect for fair resource allocation and sequential processing. Understanding both structures and knowing when to use each one is a crucial skill for any programmer.

The implementations we've explored show that you can build these structures using arrays or linked lists, each with its own trade-offs. Array-based implementations offer better cache locality but have fixed size limitations, while linked list implementations provide dynamic sizing but use more memory per element.

As you continue your programming journey, you'll find these data structures appearing everywhere – from simple algorithms to complex system designs. Master them well, and you'll have powerful tools at your disposal for solving a wide range of computational problem

FAQs

What's the main difference between a stack and a queue?

The main difference lies in their ordering principles. A stack follows Last-In-First-Out (LIFO), meaning the most recently added element is removed first, like a stack of plates. A queue follows First-In-First-Out (FIFO), where the first element added is the first to be removed, like a line at a store.
Which is better for implementation: arrays or linked lists?

It depends on your specific needs. Array-based implementations offer better performance due to cache locality and require less memory per element, but they have fixed size limitations. Linked list implementations provide dynamic sizing and no overflow issues but use more memory and have slightly slower access due to pointer traversal.
Can a stack or queue have unlimited size?

In theory, yes, but in practice, they're limited by available memory. Array-based implementations have explicit size limits, while linked list implementations are limited by system memory. It's always good practice to implement size checks and handle memory allocation failures.